Solving Sudoku puzzles with Genetic Algorithm

A long time ago (no, not in a galaxy far far away, but almost), one of my best friends told me about genetic algorithms and explained to me globally how they work. I forgot about it until I decided to learn Python.
As I was looking for both an interesting and challenging topic to learn the language, I remembered this idea and decided to reuse it.

In this post I propose you to explore what are genetic algorithms and how it works by solving sudoku puzzles as an example.

Disclaimer:

• This project is only for personal challenge and educational purpose, no other pretention than those ones.
• I could have used some libs such as pyevolve but the goal was more to understand how Genetic Algorithms works, what I am doing and why I am doing it.
• Objective was also to improve my personal skills in Python but perhaps sometimes my choices/approaches are not so 'pythonic', sorry about that.

Solving sudokus with computer: a lot of approaches are available

With a 9x9 puzzle, you should be able to solve the sudoku with another approach than deploying a genetic algorithm: Backtracking¹², Operations Research (as it is a Constraint Satisfaction Problem³), Pencil Mark.
And I am pretty sure that a lof of others exists if you have time for a little googling session.

Of course basic brute force is not an option: for a 9x9 grid puzzle, “number of essentially different solutions, when symmetries such as rotation, reflection, permutation, and relabelling are taken into account, was shown to be just 5,472,730,538“⁴. That would take ages to run.
Backtracking is also a kind of brute force search. Principle is to fill empty cells with a value that satisfies the constraints, moving forward to the next cell when it works, moving backward when there is a constraint violation. If one of its advantages it to guarantee a solution will be found, a major drawback is that solving time may be slow due to the solutions tree sequential exploration.

Pencil mark approach consists in filling all cells with possible values (i.e a value is which not already present in same row/column/grid)⁵. Some cells will have only one possible value so it is safe to assign this value to this cell. Then we start again until there is no more cell with unique value to assign. For easy puzzles, this solution is sufficient to solve them.

Using backtracking works fine for small grid sizes but becomes computationally unaffordable for larger grid sizes.
Pencil mark can help to fill some cells but it might stop because at some point there is no more cell with single value to safely assign.

So what?
Solving NxN Sudoku puzzles is known to be NP-complete. With greater size, it is not so easy and even for some 9x9 puzzles, sometimes it is difficult to solve them ‘just with logic’ and you need to bet on some answers to move on.

Note: “if a solution to an NP-complete problem can be verified quickly, there is no known way to find a solution quickly. That is, the time required to solve the problem using any currently known algorithm increases rapidly as the size of the problem grows”⁶.

Here is why we can try another approach by using a genetic algorithm.

Credit: Hans-Peter Gauster - Unsplash

What is a genetic algorithm?

Principle

Let’s start with the wikipedia definition:

“a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection.”⁷

Credit: Harshil Gudka - Unsplash

Wow….OK. Let’s try to analyze this.
The most important elements in this sentence are: “process of natural selection”, “evolutionary algorithms”, “bio-inspired operators” and “mutation, crossover and selection”.

As you may now have understood, Genetic Algorithms are inspired by the Natural selection, Darwin’s theory of evolution, according to which the natural elimination of the least able individuals in the “struggle for life” allows the species to improve from generation to generation.

Here are the steps to follow:

1. build a population of potential solutions of the problem and evaluate them according to a scoring method.
2. select best elements to become the “parents” of new solutions “children” who will have elements of the solution “father” and the solution “mother”.
3. To avoid eugenics, a certain part of the population (including the bad solutions) is even selected to be parents.
4. Finally, a dose of randomness is integrated by mutating a certain part of the new population generated.
5. Then the cycle begins again with this new population which is then evaluated to serve as parents to the next.
   And so on until the problem is solved.

Or, saying it with pseudo-code (source):

generate initial population
repeat
    rank the solutions, and retain only the percentage specified by selection rate
    repeat
        randomly select two solutions from the population
        randomly choose a crossover point
        recombine the solutions to produce n new solutions
        apply the mutation operator to the solutions
    until a new population has been produced
until a solution is found or the maximum number of generations is reached

Drawbacks

GA are pretty cool things to work with but you need to keep in mind that it is not totally magic (only a little bit). Here are some limitations, to name but a few:

• A GA might find the solution quicker than trying all possible solutions (after all, it is one of their goal) but it does not mean than it will find the solution.
• Compared to other approaches, genetic algorithm to solve sudokus seems not being a good choice. With a large enough population size or number of generations, it should most of the time solve the sudokus. But it happens sometimes, depending on the difficulty level that the program gets stuck in local minima. Then, there is no other choice than restarting it. This could take a while to run and the randomness of children creation may give different results among the different runs of the programs if the random seed has not correctly been set.
• In the end the “best” solution is only the best in comparison to other proposals. For a sudoku it is easy to evaluate as we can determine whether the sudoku is valid or not (there are rules) so it works. But for other optimization problems, we just have a solution which is the best we have found so far with absolutely no warranty that this is the best.

Building our own Genetic Algorithm!

The algorithm parameters

Credit: Markus Spiske - Unsplash

Here are the common parameters that we can set/tune when dealing with GA:

• population_size: (int) the whole population size to generate for each generation. Do not run with a too low value.
• selection_rate: (float) elitism parameter: rate of the best elements to keep from one generation to be part of the next breeders.
• random_selection_rate: (float) part of the population which is randomly selected to be part of the next breeders.
• nb_children: (int) how many children do we generate from 2 individuals.
• max_nb_generations: (int) maximum number of generations to generate. If a solution is found before, it is displayed, otherwise the best solution (but not THE solution) is displayed.
• mutation_rate: (float) part of the population that will go through mutation (avoid eugenics). You will probably need fine tuning for this one: too high value will not help to converge but too low will not allow diversity and you might get stuck with local minima (i.e the GA cannot improve and find the solution with the parents population it has at its disposal).

Note that there are some rules about those parameters:

Indeed: ((selection_rate + random_selection_rate)/ 2) x nb_children should be equal to 1.
For example:

• 25% of the best elements + 25% randomly = 50% of the population. Divide by 2 because we need 1 father and 1 mother and we have 25% that all have 4 children => 100% of a new population.
• If we set the nb_children to 5 then we have to build a combination of selection_rate + random_selection_rate that equals 20%.

I have added other parameters:

• model_to_solve: (string) name of the .txt file that contains the sudoku problem to solve.
• restart_after_n_generations_without_improvement: (int) program will automatically restart if there is no improvement on fitness value for best element after this number of generations.
• presolving: (boolean) if True, we can reduce the number of values to find in the puzzle by using a pencil mark approach. With easy grids, after the pencil mark has ran, everything will be solved and GA does not have to run.

Classes

3 classes have been developed in this program:

• Sudoku: self-explanatory, it represents the puzzle itself
• PencilMark: a class to run the technique on a given puzzle
• SudokuGA: the processor class that contains GA orchestration steps

Sudoku class

To build a puzzle, we call the constructor by passing an array of values:

s = Sudoku(values_to_set)

with, for example, values_to_set = ['0', '8', '0', '0', '0', '0', '0', '9', '0', '0', '0', '7', '5', '0', '2', '8', ....] (81 values in case of 9x9 puzzle). Each “unknown” cell is represented by the character ‘0’.

The object can be pretty printed by calling the display() method:

s.display()

which outputs in our example:

 0 8 0 | 0 0 0 | 0 9 0
 0 0 7 | 5 0 2 | 8 0 0
 6 0 0 | 8 0 7 | 0 0 5
-------|-------|-------
 3 7 0 | 0 8 0 | 0 5 1
 2 0 0 | 0 0 0 | 0 0 8
 9 5 0 | 0 4 0 | 0 3 2
-------|-------|-------
 8 0 0 | 1 0 4 | 0 0 9
 0 0 1 | 9 0 3 | 6 0 0
 0 4 0 | 0 0 0 | 0 2 0

The object has attributes to represent rows, columns and inner grids. Those elements are computed automatically once you give the initial values.
After initialization the Sudoku object contains 3 dicts where key is index of the row/column/grid and value is an array of elements in this row/column/grid:

_columns = {0: [0, 0, 6, 3, 2, 9, 8, 0, 0], 1: [8, 0, 0, 7, 0, 5, 0, 0, 4], ...}
_grids = {0: [0, 8, 0, 0, 0, 7, 6, 0, 0], 1: [0, 0, 0, 5, 0, 2, 8, 0, 7], 2: [0, 9, ...}
_rows = {0: [0, 8, 0, 0, 0, 0, 0, 9, 0], 1: [0, 0, 7, 5, 0, 2, 8, 0, 0], ...}

We also keep note of what and where were the originally known values (so that mutation process cannot move a value that was given).
This is also a dict where key is a couple of index for row and column and value is the originally known value.

_fixed_values = {'[0|1]': 8, '[0|7]': 9, '[1|2]': 7, '[1|3]': 5, '[1|5]': 2, ...}

'[0|1]': 8 means that on the row 0, column 1 (so first row and second column) the value is fixed and it is a 8.

We have 2 different methods that fill the puzzle with some values:

• fill_random(): used when building the first population by just filling the blanks
• fill_with_grids(): some grids are given (9 if 9x9 puzzle) and a new puzzle is built upon that (rows, columns and grids). This is used when building a “child” from “parents”.

In the end 2 methods directly linked to the Genetic Algorithm aspect that will be discussed later:

• fitness(): the scoring method
• swap_2_values(): the method called by the mutation process

PencilMark class

This class is light and simple and allows us to run the pencil mark process. In the constructor, we pass the sudoku to solve:

s = Sudoku(values_to_set)
p = PencilMark(s)
p.run()

Here is the Pencil mark method:

• each cell of the puzzle has an array of boolean values all initialized to True.
• each of the boolean represents the digit (from 1 to N = objects size). Having the boolean set to True means that this value is allowed.
• for each known value we put other boolean representing other digits to False in same row, column, grid
• then we can iterate over cells and if at some position there is a single True value it means:
  • either it is a fixed one (i.e known at the beginning)
  • or a predetermined one (i.e there is no option that this value). In this case we can add this new found value
• We have now potentially new guessed values and we start again and again this process until no new cell can be guessed anymore.

Note: the PencilMark class modifies the given Sudoku.

SudokuGA class

This class contains all the steps to launch the Genetic Algorithm:

sga = SudokuGA(population_size, selection_rate, random_selection_rate, nb_children, max_nb_generations,
               mutation_rate, model_to_solve, presolving, restart_after_n_generations_without_improvement)
sga.run()

Inside SudokuGA: let’s define our genetic operations

As per the peuso-code we have seen earlier, here are the operations we have to implement and adapt to our specific problem.
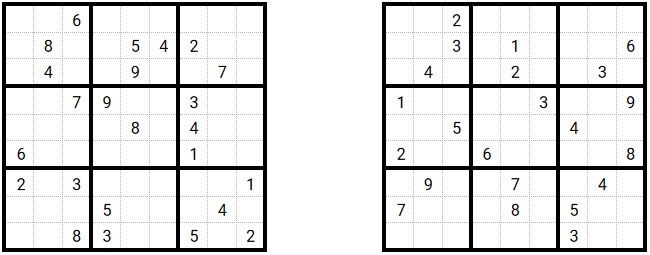
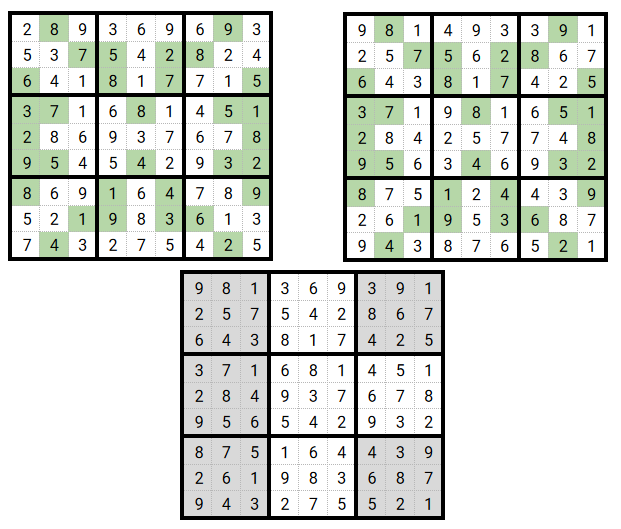
For the rest of this section we will assume that the sudoku we have to solve is this one:

Fig.1: the initial puzzle we have to solve

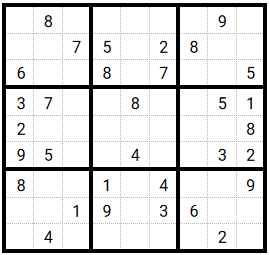
Create the first population

Fig.2: Example of one individual randomly generated

Here we just randomly generate some ‘solutions’ to evaluate. If we want our algorithm to converge, we have to help it a little bit so the creation of one individual is not totally random: the approach is to generate a potential solution with no duplicates in grids. But of course, there can be (and for sure there are) duplicates in rows and columns.
We will see just after why having no duplicates in grids is a prerequisite.

In green: the cells with ‘fixed’ values that cannot be replaced by our random generation process. We can see that grids are all valid (i.e no duplicates) whereas there are duplicates in rows or columns.

Ranking

By convention, the scoring/ranking method is called “fitness” but actually you can call it whatever you like.

This is the most important thing to think about when dealing with GA because this will determine how we will evaluate our solutions, so which ones will be selected. A bad choice and poor solutions might be chosen to be parents for the next generation…leading us in the end to very bad results.
So what could be a good and smart way to evaluate our sudoku?
In our case the fitness function counts duplicates in the potential solution: how many duplicates can be found in rows and columns overall? (there are no duplicates in grids because they have been generated without duplicates, and I paid attention to keep this always true).
So our objective is to minimize this score: the best individuals have a low fitness value (meaning there are few duplicates).

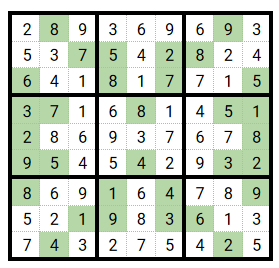
Create a child

Fig.3: first method used to create a child from 2 parents

Two potential solutions are chosen randomly and generate n children (remember that n is a parameter to set).
What we have to do is to take some elements from the father and others from the mother. But how?

For that we randomly choose a ‘crossover point’: my first decision was to take x rows from father solution and y from the mother but with such an approach there were no warranty that the child would be valid as there could be (and most of the time there would) some duplicates within grids. So I changed my mind and decided to take complete grids and we put in the child grids the father’s grids when they are before the crossover point and mother’s grids which are after the point.

Darker cells are the ones coming from the “mother” which is the sudoku on the right.

Note: the child generation is typically something that we have to pay attention to when building the algorithm because if it is not relevant, our algorithm will fail to converge.
For this sudoku specific problem, I just paid attention to have a least one grid from mother (i.e the child solution cannot be totally the same as its father).
There is a lot of room for improvement here. For example we could choose to keep the parents if their fitness value is better than their child’s one.

Mutation

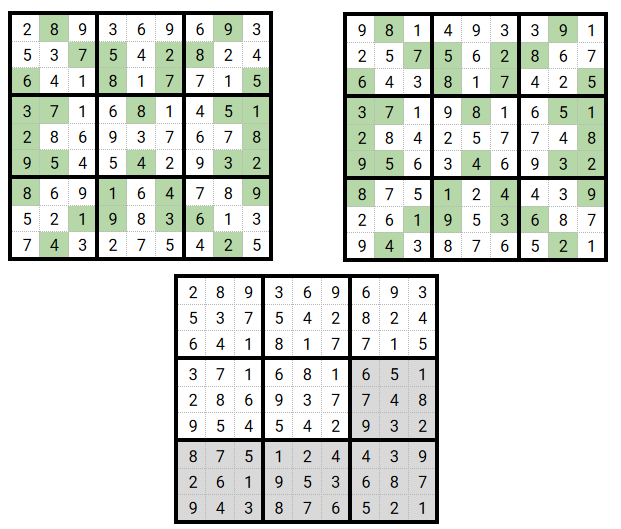
Fig.4: example of child mutation

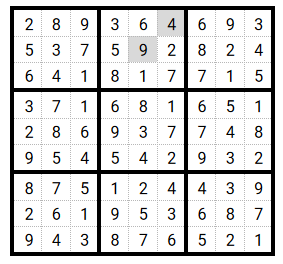
A certain percentage of the population will mutate (remember that this is also a parameter to set).
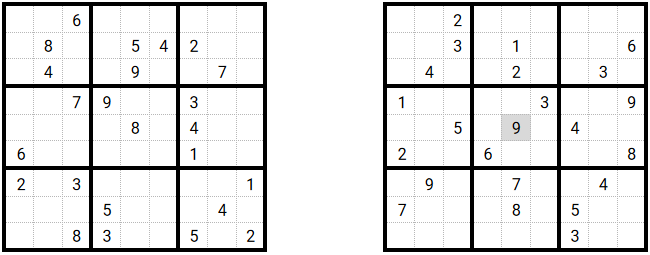
Applied to the sudoku solving problem, I chose to randomly pick one grid and, within this grid, randomly swap 2 values. The swap is made in a way that it is not allowed to swap a ‘fixed value’, i.e a value that is known and provided).
With such a mutation approach we can guarantee that grid remains coherent and without duplicates but fitness evaluation of a ‘mutated’ child is different than the one from the same element before its mutation. It can have improved it or not.

Darker cells are the ones that have swapped. The child is the one that was shown on fig. 3. You can see that the 9 and 4 have changed their place during the mutation process. All other values stayed at their place.

Fitness scores

Here are the scores for the fitness evaluation for figures 2 to 4:

• Fitness evaluation for father is 50
• Fitness evaluation for mother is 44
• Fitness evaluation for child is 41
• Fitness evaluation for mutated child is 39

We can observe that here the evolution process works, i.e the child has a lower value for the fitness value but it will not always be the case.

---

Enough talking, let’s try it!

Start with easy puzzles

Let’s start with easy puzzles that contains 43 and 49 values to find:

Fig.5: puzzles with 49 (left) and 43 (right) values to find

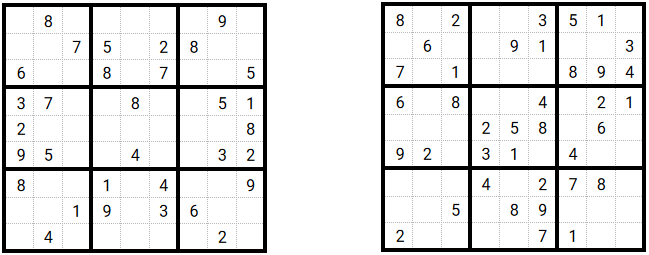
Applying Pencil Mark technique solves them instantly:

Fig.6: Pencil Mark applied on those puzzles

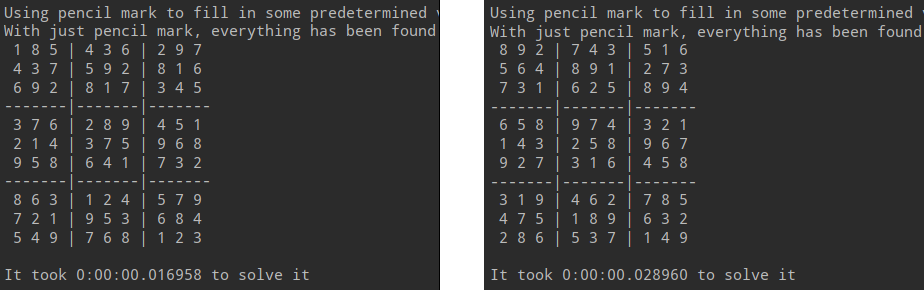
Solve with GA!

The program has been launched with those parameters:

• --population-size: 5000
• --selection-rate: 0.25
• --random-selection-rate: 0.25
• --children: 4
• --mutation-rate: 0.25

Fig. 7: Puzzles solved with GA

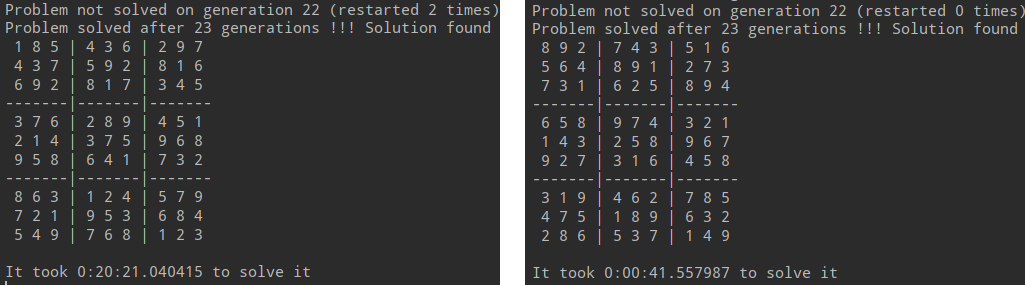
The puzzle on the left (49 guess) is more demanding for our GA but it managed to solve it after 20 minutes and around 650 generations (2 restarts) whereas the second puzzle is solved in less than one minute after 22 generations only!

Below are figures showing the evolution of fitness value for both best and worst solutions over the generations. We can see that the algorithm converges well.

Puzzle with 43 guess

Fig. 8: Evolution of fitness values over generations with population=5000 (left) and population=10000(right)

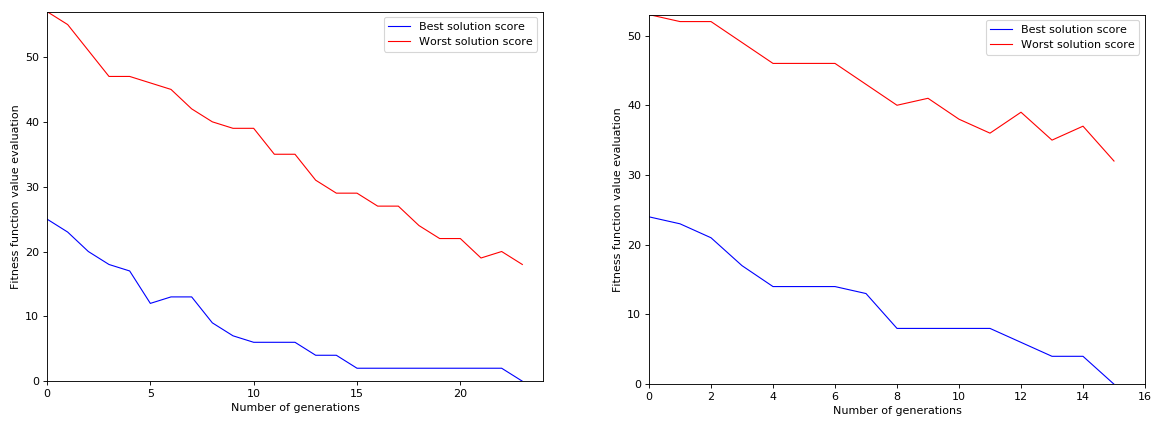
It took it few generations to get out the local minima of fitness=2.
Changing the population parameter value from 5000 to 10000 we can observe that the number of generations decreased but not so much.

Puzzle with 49 guess

Fig. 9: Evolution of fitness values over generations with population=5000 (left) and population=10000(right)

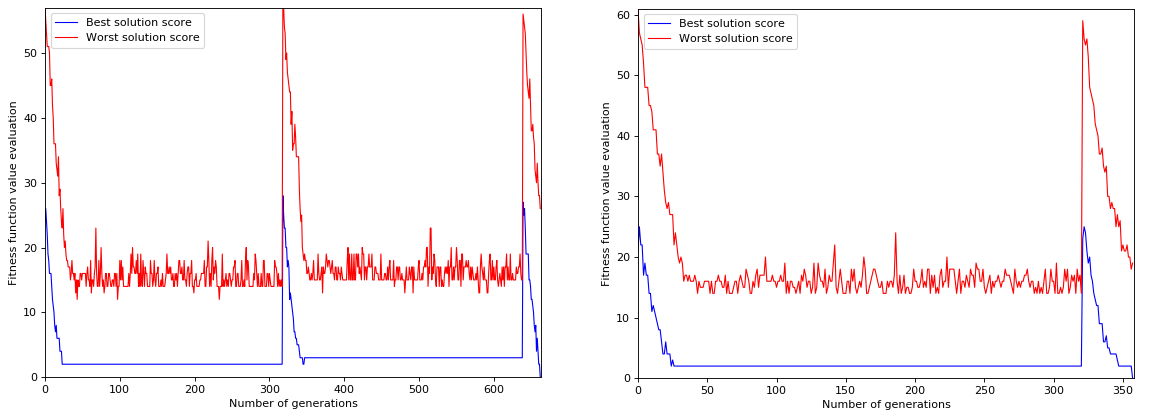
We can see that the algorithm were stuck in the local minima until the program restarted. Of course we can tune the restart_after_n_generations_without_improvement parameter value in order to decrease the waiting time but here is one of the main drawback of this kind of algorithm: it can take a while to figure out the solution. Note that here it is total luck as the restart does not keep the best elements from the previous runs (this could be one of the further improvements).
Changing the population parameter value from 5000 to 10000 we can observe that the number of generations decreased but there were still one restart.

How good can it be? Let’s try with harder 9x9 puzzles!

I will try to solve 2 harder puzzles with respectively 57 and 59 cells to find.

Fig.10: puzzles with 57 (left) and 59 (right) values to find

Applying Pencil Mark technique cannot help so much (on the left, it cannot place a single “new value”):

Fig.11: Pencil Mark applied on those puzzles

Solve with GA!

The program has been launched with those parameters:

• --population-size: 20000
• --selection-rate: 0.25
• --random-selection-rate: 0.25
• --children: 4
• --mutation-rate: 0.25
• --restart-nb-generations: 30

Changes are on the population_size and the restart-nb-generations (to decrease waiting time as it might restart several times).

Puzzle with 57 guess

Fig. 12: hard puzzle solved with GA

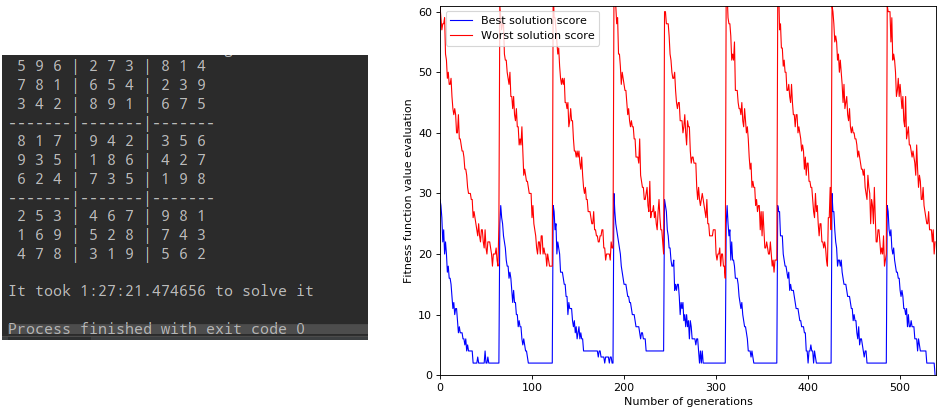
This is very demanding for our GA but it managed to solve it after 1.5 hour and around 550 generations (8 restarts)!
Here the strategy for children generation has changed a little: for each child parents were randomly chosen (instead of each couple father/mother giving birth to nb_children children). Note that I did not try to launch it with the previous strategy so maybe it works as well.

Puzzle with 59 guess

Fig.13: GA could not find the solution

Unfortunately, after few hours of running, it did not manage to find the solution for this puzzle. I have tried:

• both strategies for children generation: nb_children per couple or all children with random parents
• to change the number of children (from 4 to 5)
• to increase the mutation rate to add more diversity
• to increase the population size to generate more potential solutions per generation

It did not work. In this configuration, the GA did not manage to solve this hard puzzle.

So I tried another change in the child creation process: instead of taking randomly only one crossover point I chose:

• m, a random number of grids to take from the mother (from 1 to 8 - again to ensure having elements from both parents)
• m randomly chosen grids ids.

Then, to build the child, when iterating over grids, if the grid id is one of the mother it is taken from this sudoku otherwise it comes from the father.

Example for a better understanding: imagine here that m is randomly set 4 and that the m random values are [0, 2, 3, 6] (remember that elements follow 0-based indexing). That would give:

Fig.14: new way to create a child from 2 parents

Does it work?

Fig. 15: hard puzzle solved with GA

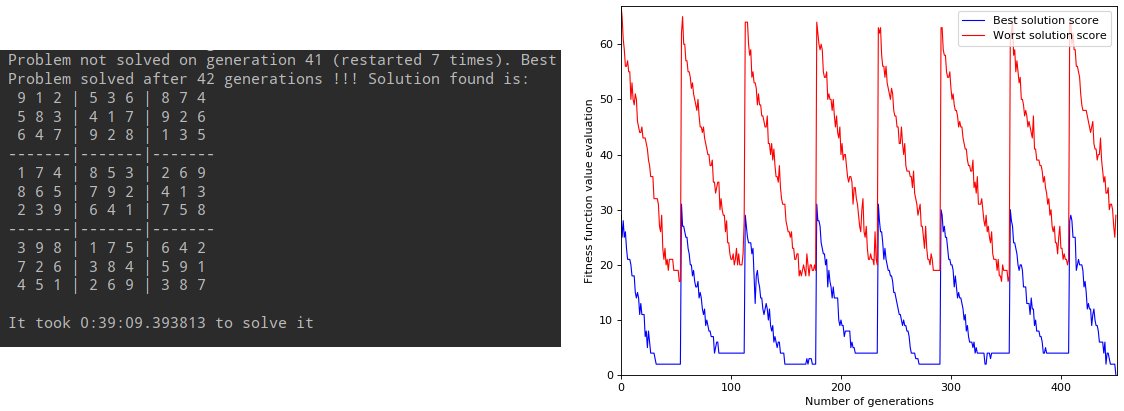
It took less than 40 minutes to find one solution!

This new child generation method has been tried on the previous sudoku and results were highly improved as well: it tooks 36 minutes instead of 1.5 hour, we can conclude that this method is better so we can keep it.

Can it solve a 4x4 puzzle grid?

Fig.16: bigger puzzle to solve

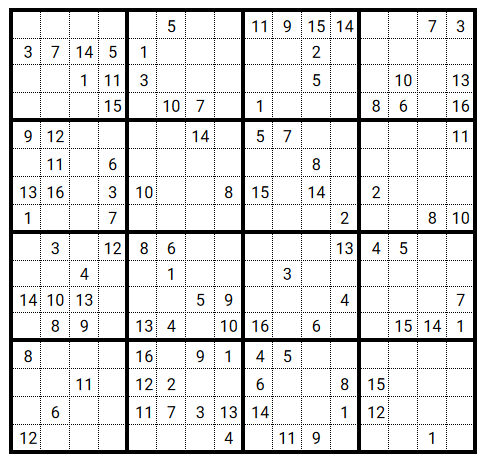
Still OK for Pencil Mark technique, puzzle solved automatically:

Fig. 17. 4x4 puzzle solved with Pencil Mark technique

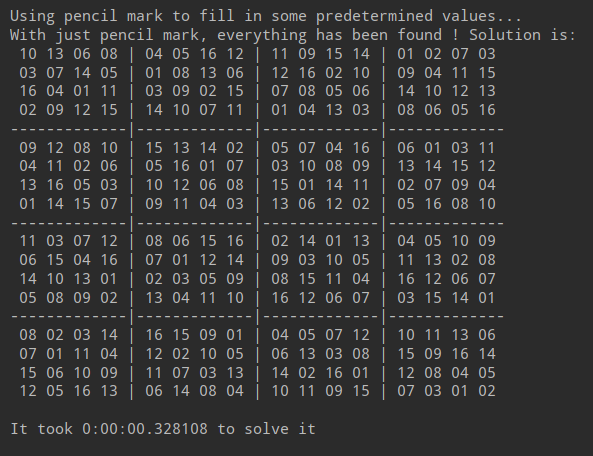
Try to solve with GA!

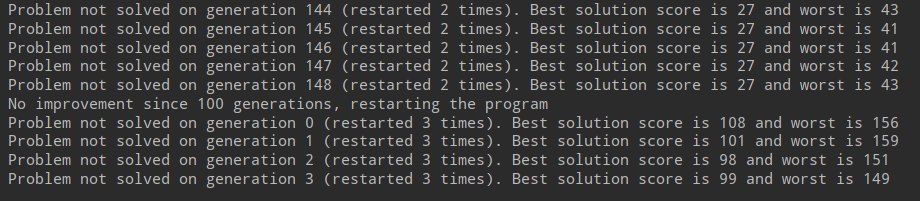
The size of the puzzle increased the complexity of the algorithm which did not manage to solve it.

---

Credit: Rick Mason - Unsplash

WRAP-UP

We have discovered the main principles of Genetic Algorithms and how they work through a fun example with Sudoku puzzles.
We have also faced the common issues with such algorithms: computation time with no guarantee to find the solution.
Moreover, in our particular case, if the solution is not found, there is little chance that we can take the best solution found as a new start: changing the remaining duplicated value could violate other constraints and so the whole potential solution becomes something very far from the real solution.
We have seen that increasing the problem complexity (4x4) could bring issues to find the solution (whereas other techniques can solve instantly).

Possible further improvements:

• change the child creation method with perhaps another crossover point to mix more elements from father and mother
• keep the parents if their fitness value is better than their child’s one
• keep best elements from previous generation when algorithm restarts

Thanks for reading.
Author: nidragedd

---

If you would like to check out the whole project you can see it from my Github repository.

---

1. Principle of Backtracking ↩

2. See the great animation picture on wikipedia for a better understanding of how backtracking works. ↩

3. What are Constraint Satisfaction Problems ↩

4. Number of solutions for a 9x9 grid ↩

5. Principle of Pencil Mark ↩

6. NP-Complete problems ↩

7. Genetic Algorithm wikipedia page ↩